VCR Redux - Net Expected Utility Derivative
Recap
In the previous article the VCR (value/cost ratio) was introduced as a way to determine when potential investment scenarios are favorable (i.e. you can actually gain more utility by winning than what it costs to play). The example scenario was the lottery, and it was suggested that a $\text{vcr} > 1$ could be favorable. The key word there is could. In fact what we saw in the previous article suggested that you actually need to know if the net expected utility $E(n)$ will be increasing or decreasing to really know if it is favorable to play (see below for $E(n)$ equation):
If $E(n)$ was increasing from $n = 1$ onward, then it was possible to increase your net expected utility by playing repeated trials of the game (e.g. in the lottery scenario this meant buying more tickets, as each ticket represented a repeated play of the game). If $E(n)$ decreased, then the highest possible net expected utility could only be achieved at $n = 1$.
The Derivative
To state this more plainly, if the first derivative of $E(n)$ is positive, then it should ultimately be favorable:
\[\frac{dE(n)}{dn} > 0\]Else if the first derivative of $E(n)$ is negative, it should not be favorable:
\[\frac{dE(n)}{dn} < 0\]And the actual first derivative of the $E(n)$ equation:
\[\frac{dE(n)}{dn} = -p^n \ln(p) U - C\]And substituting for the first derivative equation and rearranging we have a favorable outcome:
\[\frac{-p^n \ln(p) U}{C} > 1\]And a not favorable outcome:
\[\frac{-p^n \ln(p) U}{C} < 1\]Retry
Now let us attempt to retry the previous example investment data from the previous article and see what happens:
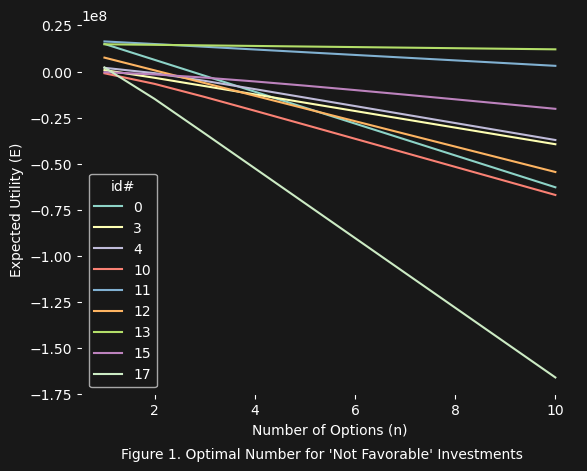
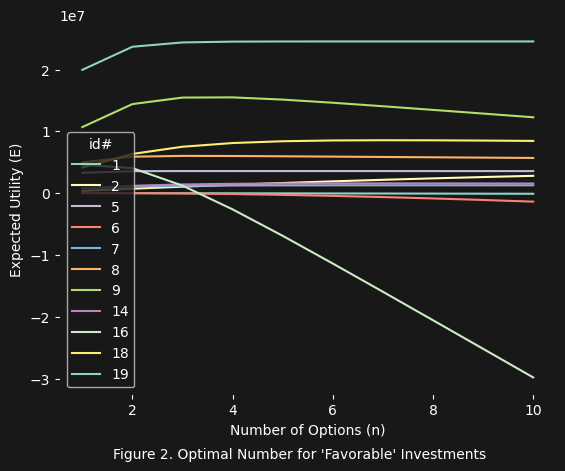
The two figures above show the results of using the new VCR equation based on $\frac{dE(n)}{dn}$ (shown below):
\[\frac{-p^n \ln(p) U}{C}\]This new VCR equation works extremely well to indicate which investments are favorable, not just in terms of having a positive net expected utility but also having an optimal options value $n$. In truth one could simply just use the $\frac{dE(n)}{dn}$ equation evaluated at $n = 1$ to make the same judgement (this can be seen in the table below, where all values E(n), dE/dn, and vcr_redux are evaluated at $n = 1$).
U C p E(n) dE/dn vcr_redux
id
0 23628740 8645440 0.000746 1.496568e+07 -8.518562e+06 0.014676
1 37439 13078 0.464476 6.971483e+03 2.570710e+02 1.019657
2 19653650 288621 0.966351 3.727013e+05 3.614480e+05 2.252328
3 5627542 4508619 0.060871 7.763714e+05 -3.549815e+06 0.212660
4 8921652 4610030 0.258521 2.005189e+06 -1.489936e+06 0.676806
5 3589078 1369 0.080797 3.297723e+06 7.281836e+05 532.909132
6 7242285 543692 0.920817 2.977158e+04 6.443215e+03 1.011851
7 1284134 890 0.415387 7.498308e+05 4.677367e+05 526.546849
8 6244378 54235 0.192862 4.985840e+06 1.927784e+06 36.545012
9 18311837 602570 0.382745 1.070051e+07 6.128551e+06 11.170687
10 9287015 7629121 0.281932 -9.604124e+05 -4.314111e+06 0.434521
11 17871191 1479129 0.004422 1.631303e+07 -1.050697e+06 0.289652
12 14431905 6896584 0.000053 7.534556e+06 -6.889056e+06 0.001092
13 15094491 306069 0.000551 1.478010e+07 -2.436473e+05 0.203946
14 1709084 14159 0.528880 7.910248e+05 5.616199e+05 40.665224
15 5991814 2618516 0.623773 -3.642328e+05 -8.545172e+05 0.673664
16 16564190 4638472 0.441722 4.608952e+06 1.339872e+06 1.288861
17 23161105 18919224 0.089064 2.179065e+06 -1.393051e+07 0.263685
18 9198955 71751 0.542063 4.140790e+06 2.981794e+06 42.557520
19 24563207 271 0.187116 1.996676e+07 7.703036e+06 28425.487632
Notice how in the above table, everywhere that dE/dn $< 0$ the vcr_redux $< 1$? Again, you can simply use the $\frac{dE(n)}{dn}$ equation evaluated at $n = 1$ to get the same results as the new VCR equation (vcr_redux). Also notice that everywhere that $E(n)$ (evaluated at $n = 1$) is negative in the above table, the corresponding $\frac{dE(n)}{dn}$ is also negative.
Moral
As it turns out, a little calculus can tell us a lot about what a function is doing. In this specific application, it allows us to determine when a specific set of U, C, and p values not only yield a positive net expected utility (i.e. $E(n) > 0$) but whether this particular investment has a maximum value somewhere in the range $n > 0$ (meaning that there is possibility for purchasing $n >=1$ options to increase $E(n)$.