Optimal Options - Options Advantage in Practice
Considering Cost
In our first article on the advantage of options we showed that the probability of winning at least once $P(\text{win})$ would increase (approaching unity) as the number of options $n$ went to infinity:
\[\lim_{n \to \infty} P(\text{win}) = \lim_{n \to \infty} \left(1 - \prod_{i=1}^{n} P(\text{lose})_i \right) = 1\]But this only applies to the probability and does not take into consideration the cost of each additional option and the payoff upon winning. Instead if we consider the cost $C$ and the payoff/utility $U$ of winning a single option, we then arrive at an updated version of the equation introduced in the previous article:
\[E(n) = (1 - p^n)U - nC\]What we have now is an equation that calculates the net expected utility (i.e. difference between the expected utility $(1 - p^n)U$ and the total options cost $nC$).
The “Ideal” Lottery
As an example demonstration of this equation’s power, let us consider an ideal lottery with the following criteria:
- $U = 20,000,000$ USD is the grand prize
- $C = 2$ USD is the cost per ticket
- $p_w = \frac{1}{2,550,000}$ is the probability of winning $p_w$ per ticket
So then what we want to know is what value of $n$ makes this advantageous (i.e. greater than zero):
\[E(n) = (1 - \frac{2,549,999}{2,550,000}^n) \cdot 20,000,000 - 2n > 0\]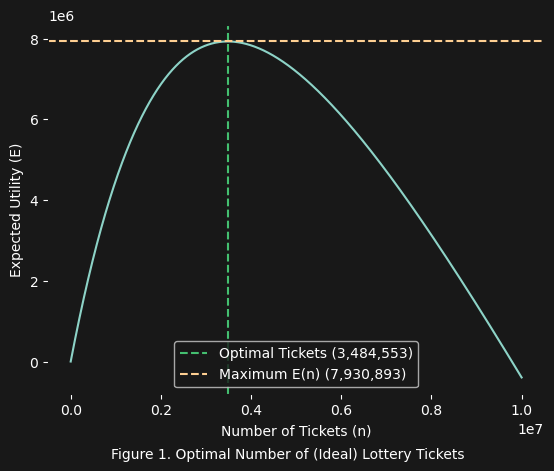
As it turns out, this “ideal lottery” is quite advantageous, as you can see in figure 1 above. There is even an optimal number of tickets $n$ where $E(n)$ (the expected utility) is maximized. This occurs at $n = 3,484,553$ and yields a maximum expected utility:
\[\begin{align*} E(n) &= (1 - \frac{2,549,999}{2,550,000}^n) \cdot 20,000,000 - 2 \cdot 3,484,553 \\ &\approx 7,930,893 \end{align*}\]The REAL Lottery
But this is where the “fantasy” ends and the reality begins. Let us consider the same lottery example shown above, but this time we increase the price of each ticket $C$ to $100$ USD:
- $U = 20,000,000$ USD is the grand prize
- $C = 100$ USD is the cost per ticket
- $p_w = \frac{1}{2,550,000}$ is the probability of winning $p_w$ per ticket
So what would we expect to happen now?
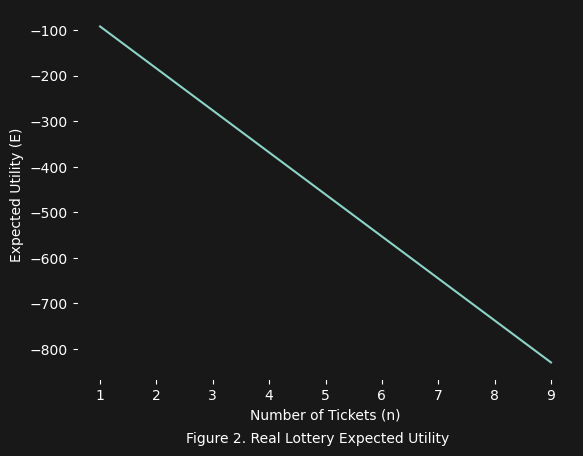
What we see is that basically the expected utility is never going to be positive (i.e. you are losing instead of winning). Every ticket you buy costs you more than what you can “expect” to win. This is the power of the cost $C$ of each additional option. In the previous “ideal” lottery, it was only the lower cost of $2$ USD that made it advantageous to buy ANY number of tickets. Now with the price set to $100$ USD, there is no real winning … only losing.
Moral
While it is certainly true that buying more tickets for the lottery will increase your probability of winning, but it will NOT increase your expected utility and hence your profit. In fact you will be in a worse position after buying $n >= 1$ tickets, because you will now be $100 \cdot n$ less wealthy. This example perfectly illustrates why only considering the probability of winning, and not factoring in the utility is an ultimately incomplete calculation. Utility must be considered for any situation where advantage is the desired calculation.