Value to Cost Ratio - Higher Level Investment Decisions
Favorable Investment Detection
In the previous article, the following equation was defined and used to calculate the net expected utility:
\[E(n) = (1 - p^n)U - nC\]In the article, a lottery example was used to demonstrate the equation and show objectively which scenario was more advantageous. But this required a much more intensive computation, all to simply show that the second scenario (i.e. the “real” lottery) was completely unfavorable. Is there a better way to determine if some investment is favorable before calculating out the optimal options number $n$?
The Ratio
Consider the following problem: you have a series of investments with known $U$, $C$, and $p$ values, which ones do you choose to further investigate the optimal options number $n$? When this collection of investments is small you can use the original net expected utility equation, but what if you have a non-trivial amount of data? Consider the following collection of investments that require some high-level decision on which are more favorable:
U C p
23628740 8645440 0.000746
37439 13078 0.464476
19653650 288621 0.966351
5627542 4508619 0.060871
8921652 4610030 0.258521
3589078 1369 0.080797
7242285 543692 0.920817
1284134 890 0.415387
6244378 54235 0.192862
18311837 602570 0.382745
9287015 7629121 0.281932
17871191 1479129 0.004422
14431905 6896584 0.000053
15094491 306069 0.000551
1709084 14159 0.528880
5991814 2618516 0.623773
16564190 4638472 0.441722
23161105 18919224 0.089064
9198955 71751 0.542063
24563207 271 0.187116
Looking at the above list of investment data can you tell which are more favorable? Should we go through the process of evaluating the net expected utility equation for each pair of $U$, $C$, and $p$ values? No we should not. Instead we should apply the following equation:
\[\frac{(1 - p)U}{C}\]The above equation is a type of risk/reward ratio (in this case reward/risk) and it can be used to get a sense of when a potential investment is favorable (or not).
Return of the Lottery
Now let us apply the previous value/cost ratio to the lottery data from the previous article:

From figure 1 it seems like the threshold for an investment to become favorable is that the value/cost ratio must exceed $1$:
\[\frac{(1 - p)U}{C} > 1\]This would make sense, because this corresponds to the following equation:
\[(1 - p)U = C\]Which is to say that the value and cost terms are equal and when evaluated normally:
\[E(n) = (1 - p)U - C = 0\]So in this case your $E(n) = 0$, i.e. you will not be winning… but at least you will not be losing (i.e. $E(n) < 0$).
Application
Finally we can apply the value/cost ratio to our example investment data and see which are favorable:
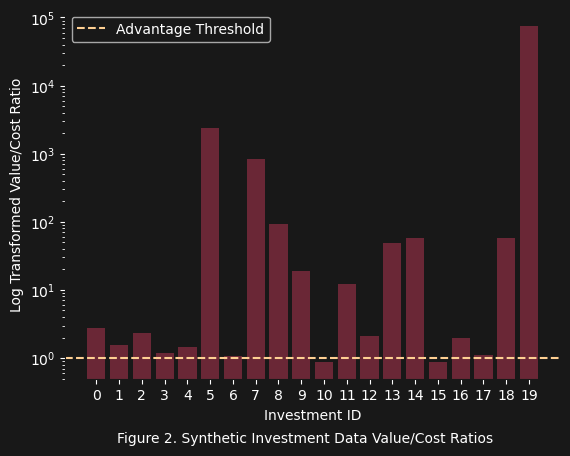
Looking at figure 2 we can easily discern which investments are not favorable, which are barely favorable, which are a little favorable, and finally which investments are reasonably and significantly favorable. But let us now actually apply the original net expected utility and reaffirm that our method works by providing some additional evidence.
Bonus Round
Now let us see how accurate our little value/cost ratio actually is. We will plot the optimal options of the investment data, by grouping them based on their value/cost ratio ($\text{vcr}$) as follows:
not favorable($\text{vcr} < 1$)barely favorable($1 < \text{vcr} < 10$)little favorable($10 < \text{vcr} < 100$)reasonably favorable($100 < \text{vcr} < 5000$)significantly favorable($\text{vcr} > 5000$)
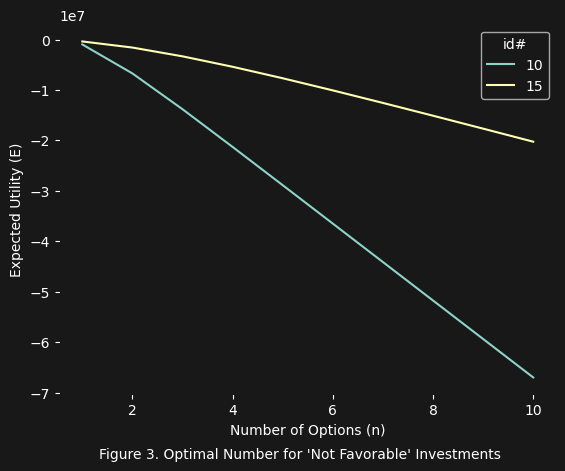
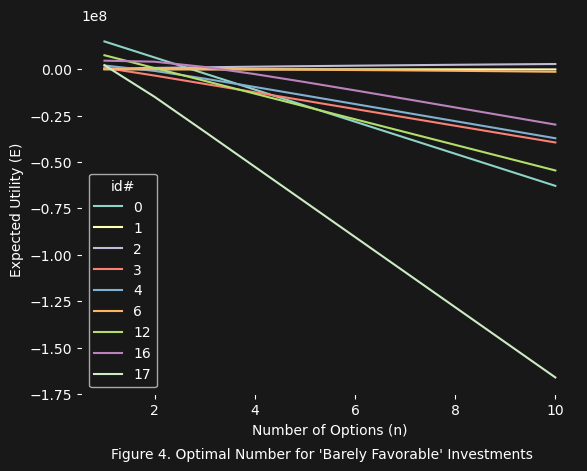

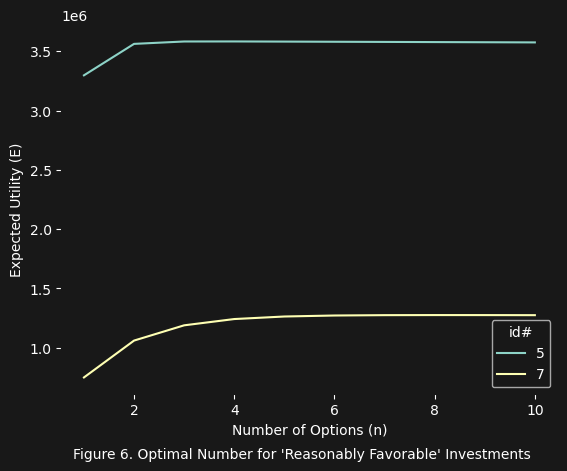
The results are quite interesting (see below data table for investment id lookup). In figure 3 we see basically what we expected (i.e. nothing favorable). In figure 4 there is something interesting happening with the investment ids $1$, $2$, and $6$. And finally in figures 5, 6, and 7 we see what we would expect (several favorable investment options). Of course we also realize from these figures the limits of the value/cost ratio: the ratio alone is not enough to completely filter investment options, unless these options have a $\text{vcr} < 1$ (i.e not favorable). If the $\text{vcr} > 1$, then the particular investment could be favorable. However, the net expected utility equation is still needed to figure out if $E(n)$ decreases as $n$ increases, and if it increases, what the optimal number of options (e.g. the tickets in the lottery) will be.
U C p vc_ratio
id
0 23628740 8645440 0.000746 2.731049
1 37439 13078 0.464476 1.533070
2 19653650 288621 0.966351 2.291317
3 5627542 4508619 0.060871 1.172197
4 8921652 4610030 0.258521 1.434962
5 3589078 1369 0.080797 2409.855075
6 7242285 543692 0.920817 1.054758
7 1284134 890 0.415387 843.506572
8 6244378 54235 0.192862 92.930296
9 18311837 602570 0.382745 18.758112
10 9287015 7629121 0.281932 0.874112
11 17871191 1479129 0.004422 12.028809
12 14431905 6896584 0.000053 2.092506
13 15094491 306069 0.000551 49.290101
14 1709084 14159 0.528880 56.867280
15 5991814 2618516 0.623773 0.860901
16 16564190 4638472 0.441722 1.993636
17 23161105 18919224 0.089064 1.115177
18 9198955 71751 0.542063 58.710553
19 24563207 271 0.187116 73679.074749
Moral
The power of numbers is not just their objectivity, but also in their ability to obfuscate the truth. As paradoxical as this may sound, what else could be said in regards to the example investment data? It is simply not a simple task to look at columns of numbers and directly determine which will be more favorable in their net expected utility by first impression alone. It is only through a more sharpened application of mathematics (and hence the mind) that we can extract from this infinitude of numbers that mysterious and obscure truth that we desire above all: which investments are favorable?