Visa Advantage - Visa Strategies for Wealth Management
Visa Types
When it comes to traveling and living abroad in general, one of the major decisions one must make is related to the visas used to enter the desired country. Basically all visas can be grouped into two basic categories:
- Long-Term
- Short-Term
The difference between the two is simply the duration of stay. As you could imagine long-term visas entail at least a year or more stay, where as short-term are at most 3 months. Thus different strategies are needed depending on the type of visa you choose.
Long-Term Visa Strategies
Since the long-term visa will typically include at least a year or more of duration in the foreign country, we can begin to understand the advantage in terms of the additional months $\Delta{N}$ acquired by residing/operating in the foreign country compared to the country of origin:
\[\Delta{N} = N_{foreign} + N_{remainder} - N_{domestic}\]Where $N_{foreign}$ is the total number of months that your wealth $W$ can purchase for you under a given cost of living $C$, $N_{remainder}$ is the remaining wealth (if any) that will be used to live in the country of origin upon return from the foreign country, and $N_{domestic}$ is simply the numer of months that your wealth $W$ can purchase for you under the cost of living $C$ in your home country (never having traveled to the foreign country). The full equation is shown below:
\[\Delta{N} = \min\left(\frac{(1 - p)W}{C_{f}}, N_{limit}\right) + \frac{(1 - p)W - \min\left(\frac{(1 - p)W}{C_{f}}, N_{limit}\right)C_f}{C_d} - \frac{W}{C_{d}}\]Where the $C_{f}$ and $C_{d}$ terms are the cost of living (including renting, utilities, food, etc …) for both the foreign and domestic countries respectively. The value $(1 - p)W$ is the remaining wealth after $pW$ is used to pay various costs related to travel $T$, visa fees $V$, investment $I$, etc … into the target foreign country:
\[pW = T + V + I \dots\]The term $N_{limit}$ is the maximum amount of months the specific visa allows, and if the $(1 - p)W$ term can purchase more months (with cost of living $C_f$) than $N_{limit}$ allows, then the smaller of the two values (i.e. $N_{limit}$) will be chosen. That is the purpose of this component of the equation:
\[\min\left(\frac{(1 - p)W}{C_{f}}, N_{limit}\right)\]And of course $p$ is the fraction of wealth used to cover the necessary costs (i.e. travel, visa fees, investment, etc …) for entering and residing in the target foreign country.
Brazil
As an example of the long-term visa strategy, let us look at the average U.S. citizen circa 2022 (who you may recall has $\sim62\text{k}$ USD in savings) residing $1$, $2$, $4$, and $8$ years in Brazil.
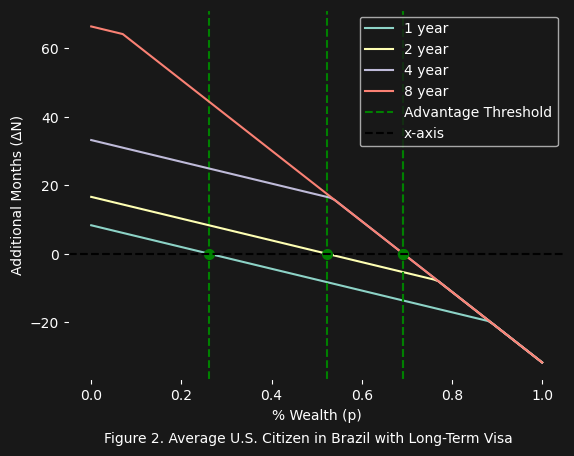
Figure 2 shows some interesting results. Naturally it makes sense that as the visa duration $N_{limit}$ increases from $1$ to $8$ years, the additional months $\Delta{N}$ gained increases (because you are not limited by the visa’s duration and can buy more time at a lower $C_f$ in the foreign country). But what is the nature of the strange “angle” or “kink” in each line? As it turns out, everything preceeding this “kink” is the result of the remaining wealth $(1 - p)W$ exceeding $N_{limit}$:
\[(1 - p)W > N_{limit}\]Naturally, everything to the right of this “kink” is the result of the remaining wealth being less than $N_{limit}$:
\[(1 - p)W < N_{limit}\]As $N_{limit}$ increases from $1 - 8$ years, we see the kink shift to the left. Why? Again, because more and more of your remaining wealth $(1 - p)W$ can be used to buy more months $N$.
Another key insight worth pointing out is that everything below the x-axis (i.e. when $\Delta{N} \lt 0$) is no longer favorable. Why? Because the % wealth $pW$ you set aside for travel $T$, visa $V$, investment $I$, and any other costs, leaves a remaining wealth $(1 - p)W$ that buys less months $N$ than if you stayed in your home country (in this case the U.S.). To put it more clearly:
Finally, why does the “break even” point shift to the right as the visa duration increases from $1$, $2$, $4$, and $8$? Keep in mind that the equation accounts for the $N_{remainder}$ which is the amount of months that can be purchased with any wealth remaining after leaving the foreign country and returning home. So what we are seeing is, that as the visa duration increases, and you are legally allowed to reside in the foreign country for longer time, you can purchase the same amount of months for a smaller percent of your wealth. Or to put it another way, the fraction of wealth $p$ set aside for the various costs ($T$, $V$, $I$, etc …), can increase:
\[\begin{align*} \Delta{N}_8 &= \Delta{N}_4 = \Delta{N}_2 = \Delta{N}_1 = N_{foreign} + N_{remainder} - N_{domestic} = 0 \\ (1 - p_8) &= (1 - p_4) < (1 - p_2) < (1 - p_1) \\ p_8 &= p_4 > p_2 > p_1 \end{align*}\]Notice that the “break even” point for both the $4$ and $8$ year visa is the same. Why? Because they are both under their max visa duration:
\[\frac{(1 - p)W}{C_f} < N_{limit}\]And when this happens the equation simplifies to:
\[\begin{align*} \frac{(1 - p)W}{C_{f}} + \frac{(1 - p)W - \frac{(1 - p)W}{C_{f}}C_f}{C_d} &- \frac{W}{C_{d}} \\ \frac{(1 - p)W}{C_{f}} + \frac{0}{C_d} &- \frac{W}{C_{d}} \\ \frac{(1 - p)W}{C_{f}} &- \frac{W}{C_{d}} \end{align*}\]With the visa duration $N_{limit}$ no longer in the equation, the results of the $4$ and $8$ year visas are the same.
All of this is to state a very simple fact: the more time you can spend under the lower cost of living $C_f$ the more wealth $pW$ you can use on any and all costs, and the less remaining wealth $(1 - p)W$ you need to maintain the minimum months of wealth (i.e. $\Delta{N} = N_{domestic}$).
Short-Term Visa Strategies
The short-term visas are usually measured in days (e.g. $30$, $60$, $90$), and the main difference between the two strategies is that for the short-term strategy we want to combine multiple countries (their $C_f$ and $T$, $V$, $I$, costs) together to take advantage of possible advantageous combinations:
\[\begin{align*} N_{limit} &= \sum_{i=1}^n \frac{S_i}{30.4375} \\ D_{total} &= \sum_{i=1}^n \min\left(d_i, S_i\right) \\ C_f &= \sum_{i=1}^n \frac{\min\left(d_i, S_i\right)}{D_{total}}C_i \\ pW &= \sum_{i=1}^n T_i + V_i + I_i \end{align*}\]Here $S_i$ is the max visa days, $d_i$ is the days chosen to stay in the country such that $d_i <= S_i$, $D_{total}$ is the total days of residing in all countries, and $T_i$, $V_i$, and $I_i$ are the necessary costs, all for the i-th country out of $n$ total countries that will be visited for $d_i$ days.
The South America Tour
Let us now apply the short-term strategy to South America, where instead of traveling only to Brazil we will stay in multiple countries for the max visa days $S_i$ in each.
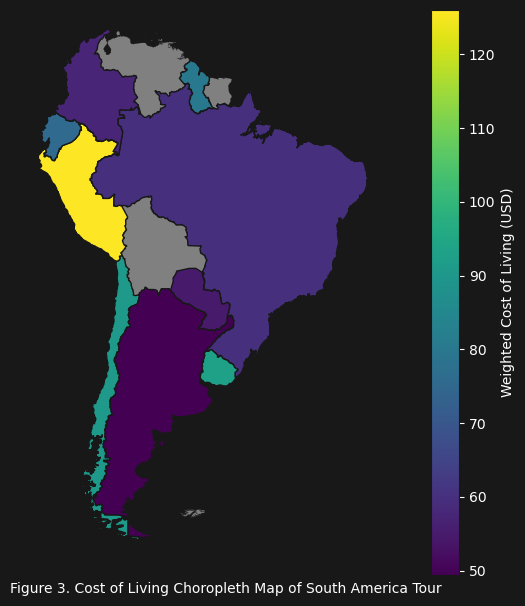
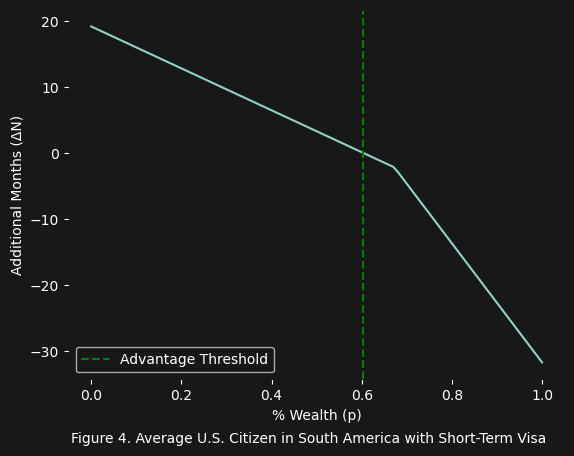
Figure 3 gives us a sense of the weight of each country’s cost of living for this trip (where the lighter the color the more weight that country’s cost of living has in the $C_f$ value). Again this is a result of the way we calculate $C_f$:
\[C_f = \sum_{i=1}^n \frac{\min\left(d_i, S_i\right)}{D_{total}}C_i\]Figure 4 shows us that, worse case scenario, the average U.S. citizen could spend $60\%$ (i.e. $0.60W$) of their wealth (in this case the average U.S. savings) on this tour, and you would have the same amount of wealth time $N$ as you would had you stayed in the U.S.:
\[N_{foreign} + N_{remainder} = N_{domestic}\]This is quite an interesting result, as it also means the average U.S. citizen only needs $40\%$ of their wealth to maintain the same amount of wealth time (in months $N$) as you would in the domestic country:
\[\frac{0.40W}{C_f} = \frac{W}{C_d}\]Moral
Once a method for calculating the advantage (in this case the $\Delta{N}$ value) is defined, it becomes possible to see the truth about whatever may be the target of the calculation. Here, we have been able to investigate the additional months $\Delta{N}$ gained by partitioning your wealth $W$ into a travel partition $pW$ and a cost of living partition $(1 - p)W$. What we can confidently state, is that there are combinations of $N_{limit}$, and $p$, that lead to significantly favorable outcomes (e.g. $\sim 3$ x increase with $\frac{N_{foreign}}{N_{domestic}}$ in the case of the Brazil long-term $8$ year visa). Further investigations into possible short-term strategies, whereby certain countries are selected due to their low cost of living $C_f$ and their relative proximity to each other, may hold significant potential advantage.