To Rent or Not To Rent - A Wealth Management Perspective
Minimizing Cost of Living
One of the major contributors to cost of living is RENT. Often rent can count for more than double the other cost of living expenses. But in order to eliminate rent, a portion of wealth must be invested into purchasing property. This could potentially decrease the number of months $N$ that you can live at your current standard of living, given your wealth $W$. So what is the optimal portion of your wealth used to purchase property so as to increase $N$?
The Basic Problem
What we are trying to find is the % wealth $p$ that maximizes the following equation:
What $\Delta{N}$ represents is the difference between the two scenarios:
\[\Delta{N} = N_{purchase} - N_{rent}\]Where $N_{purchase}$ is the number of months the remaining wealth $(1 - p)W$ can purchase under the monthly cost of living $C$, and $N_{rent}$ is the number of months the original wealth $W$ can purchase under monthly cost of living PLUS rent $(C + R)$:
\[\begin{align*} N_{purchase} &= \frac{(1 - p)W}{C} \\ N_{rent} &= \frac{W}{C + R} \end{align*}\]Now let us visualize a specific example of the basic problem. Say you have $62k$ USD in savings (the average US savings circa 2022), your rent is about $1.7k$ USD, and the cost of living is $1.2k$ USD (from Numbeo circa Q2 2024):

What figure 1 above shows is that, below $p = 0.6$ you will actually increase $N$: you will gain more time, measured in months, for your given wealth and given cost of living. Granted it also suggests, unsurprisingly, that the lower that $p$ value is, the more months $N$ you are going to get.
The Advanced Problem
The basic problem only considers the scenarios for purchasing and renting, but there is a third scenario: $N_{sell}$. This third scenario represents the number of months to be gained after selling the property purchased in the second scenario $N_{purchase}$:
\[\Delta{N} = N_{purchase} - N_{rent} + N_{sell} - N_{limit}\]Where $N_{limit}$ represents an arbitrary minimum limit of months that are worth selling the previously purchased property for. The $N_{limit}$ term is really only used to find the advantage threshold (the break even point, that delineates where you begin losing advantage), and in the previous example $N_{limit} = 0$ was the advantage threshold. The full equation takes the following form:
\[\Delta{N} = \frac{(1 - p)W}{C} - \frac{W}{C + R} + \frac{paW}{C + R} - N_{limit}\]Note the $a$ variable in the $N_{sell}$ term. This variable represents the appreciation (as a fraction) of the property. For example, if the property can only be sold at $75\%$ of the original price, then $a = 0.75$, and if the property has increased in value by $50\%$ then $a = 1.5$, and so on. The simplest scenario is when $a = 1$ which then we can simplify the definition of the $N_{sell}$ term:
\[N_{sell} = \frac{pW}{C + R}\]So now let us return to the average U.S. renter scenario described above, but this time let us consider the third scenario and set the advantage threshold to $12$ (we only want to consider selling if we can get at least $12$ months out of the sell), and $a = 1$ (no change in property value):
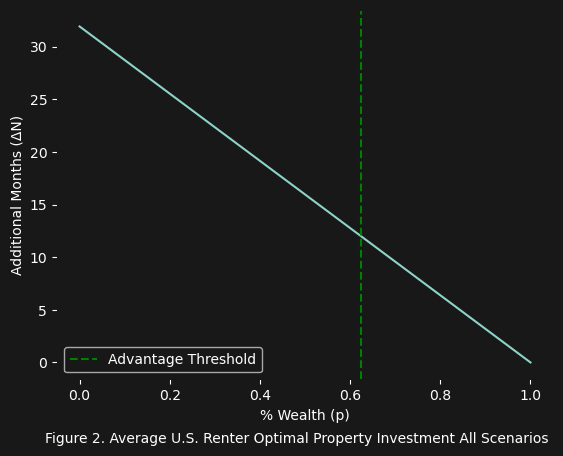
As it turns out $p \approx 0.6$ is again the optimal % wealth to use for purchasing property to eliminate rent (here it is the point where $\Delta{N} = 12$, or you are guaranteed to get at least $12$ additional months by purchasing and selling, compared to only renting). By including the selling scenario $N_{sell}$ it is even more clear how advantageous putting even $60\%$ of your wealth into purchasing real estate can be, compared to considering only the purchasing/renting scenarios (which have a $\Delta{N} = 0$ for $p = 0.6$).
Risk of Depreciation
What if $a < 1$? Meaning what if you used a fraction $p$ of your wealth to purchase property, and then when you go to sell it, you sell at a loss (i.e. lose money)?
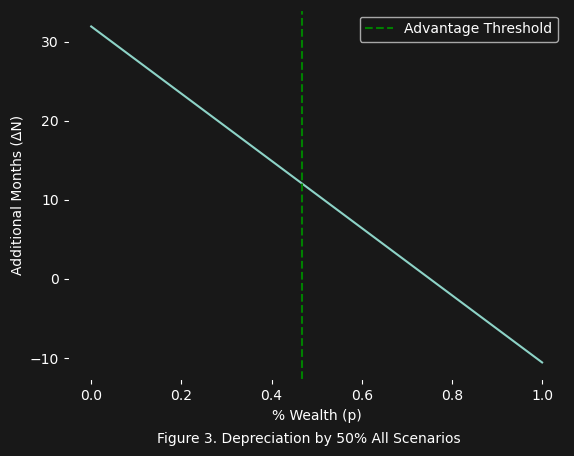
What figure 3 above shows is that even with $a = 0.50$ (i.e. a depreciation of $50\%$) you can still gain an additional $12$ more months, $\Delta{N} = 12$, compared to the number of months you can get by simply renting. In other words:
\[\begin{align*} W &= 62000 \\ R &= 1756 \\ C &= 1167 \\ p &= 0.47 \\ a &= 0.5 \\ \Delta{N} &= N_{purchase} - N_{rent} + N_{sell} = 12 \end{align*}\]So up to about $47\%$ of you wealth will allow you to get at least 12 additional months compared to the number of months possible to simply live off your wealth $W$, while paying rent $R$ and your current cost of living $C$.
Moral
In the right market (i.e the $C$, $R$, and $a$ values), with the right wealth $W$, there are circumstances where it can be overtly advantageous to purchase property using some fraction $p$ of your wealth. Granted, there are still plenty of situations where it actually does make more sense to rent (e.g. the $p$ that can increase your $\Delta{N}$ to a significant extent is not enough to actually purchase property). All things considered, it is a very straight forward calculation to determine how much more time could be purchased by your wealth, simply by eleminating rent.