Foundations of The Matching Problem - Mathematics of Matching

Big Picture

This article marks the first of many articles devoted to exploring, defining, and ultimately solving what we have come to call: The Matching Problem. This problem comes up in many different situations, and here in this article we begin to not only define what is the matching problem, but also how to define it mathematically.

Approaching The Matching Problem

As mentioned above, the matching problem is the tentative name given to a “type” of problem that occurs again and again in the problem space: how to search/optimize/select for the best match between two parties. In this linguistic definition we must clarify that when we say “parties” it can refer to anything (or anyone):

a client and a service provider (i.e. business)
individuals looking for a romantic partnership
individuals seeking the optimal career choice or “fit”
investors seeking the best assets
etc …

Basically the matching problem, in the most generalized and abstract form, involves two or more “parties” seeking some type of “match.” Both these concepts (i.e. “parties” and “match”) will need to be more objectively defined.

Profile Vectors

We can begin to “abstract” the concept of “parties” (i.e. some entity seeking a match) by thinking of each party as a tensor made of features “relevant” to the future matching algorithm (i.e. the method used to quantify/determine/measure the match percentage). The simplest tensor to start with, and aid us in our thinking, is the vector. From here on we will refer to the object that represents a “party” (i.e. a person, corporation, etc … seeking a match) as a profile vector $P$:

\[\mathbf{P} = \begin{bmatrix} p_1 \\ p_2 \\ p_3 \\ p_4 \\ \vdots \\ p_n \end{bmatrix}\]

Matching Algorithm

While the profile vector (or more generally profile tensor) is inherently more generalized and reusable amongst matching applications, the actual matching criteria (i.e. what is the metric for determining a match between two profile tensors) is a bit more specific to the application. For example, in the case where you want to match two romantic parties (e.g. a man and a woman seeking a matrimonial match), what you would be looking for is some kind of measure of similarity in their profile vectors:

\[\begin{align*} \mathbf{X}, \mathbf{Y} &= \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ \vdots \\ x_n \end{bmatrix} ,\;\; \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \\ \vdots \\ y_n \end{bmatrix} \\ \\ d \left(X, Y \right) &= \sqrt{\sum _{i=1}^{n} \left(x_{i} - y_{i} \right)^2} & \\ \\ m \left(X, Y \right) &= d \left(X, Y \right) < \delta \end{align*}\]

Where $X$ and $Y$ are the profile vectors for each “romantic” party, $d \left(X, Y \right)$ is the Euclidean distance, $\delta$ represents some distance quantity representing the threshold that once crossed (i.e. two parties and their respective profile vectors are too distant) they are not considered a match, and $m \left(X, Y \right)$ is the boolean matching operator that symbolizes the application of the matching algorithm (i.e. in this case Euclidean distance) and matching criteria and simply returns true or false (i.e. match or not match).

The use of Euclidean distance as the matching algorithm is only specific to this application. For more complex matching applications (e.g. an investor and assets) a different matching algorithm will be required.

Standard Normal / Z-Score

One of the issues encountered in working with data is normalization. When working with data, each feature often has its own scale (e.g. $[1, 100]$ or $[0, 1]$ or $[1000, 1000000]$ etc …). What we want to do is to convert the raw profile vector to something normalized (i.e. a vector where each element is in the same scale):

\[\begin{align*} \mathbf{R}, \mathbf{N} &= \begin{bmatrix} r_1 \\ r_2 \\ r_3 \\ r_4 \\ \vdots \\ r_n \end{bmatrix} , \;\; \begin{bmatrix} n_1 \\ n_2 \\ n_3 \\ n_4 \\ \vdots \\ n_n \end{bmatrix} \\ \\ \mathbf{R} &\mapsto \mathbf{N} \end{align*}\]

Here $R$ represents the raw profile vector where each feature of the vector has not been normalized, while $N$ represents the normalized version. The arrow $\mapsto$ simply designates the as of yet unknown operation for transforming $R$ to $N$ (i.e. $\mathbf{R} \mapsto \mathbf{N}$). As it turns, the method most promising is known as the standard normal or Z-score. The beauty of this method of normalization is that it does not just normalize the features to each other, but also gives you a sense of how deviant the features are from their average or distribution center.

\[\begin{align*} \mathbf{R}, \mathbf{Z} &= \begin{bmatrix} r_1 \\ r_2 \\ r_3 \\ r_4 \\ \vdots \\ r_n \end{bmatrix} , \;\; \begin{bmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \\ \vdots \\ z_n \end{bmatrix} \\ \\ \mathbf{R} &\mapsto \mathbf{Z} = z\left(\mathbf{R}\right) \end{align*}\]

Again, $R$ is the raw profile vector and $Z$ is the standard normal profile vector where each feature (i.e. element) of $Z$ is actually the Z-score for that feature. The operator $z\left(\mathbf{R}\right)$ just simply represents the standard normal operation that converts $R$ to $Z$:

\[\begin{align*} \mu &= \frac{1}{n} \sum_{i=1}^{n} R_i \\ \sigma &= \sqrt{\frac{1}{n} \sum_{i=1}^{n} (R_i - \mu)^2} \\ z\left(\mathbf{R}\right) &= \frac{\mathbf{R} - \mu}{\sigma} \\ &= \mathbf{Z} \end{align*}\]

Once in this standard normal form, we can actually compare how “normal” each feature is within the profile vector (and of course also with other profile vectors). Meaning the value of $z_1$, $z_2$, $z_n$ can all be compared to each other, allowing for an easy and instant first analysis of the “normality” of the profile vector. For example if we summed all the features and divided by the number of features, this would actually tell us how “normal” this particular profile is:

\[\bar{z} = \frac{1}{n} \sum_{i=1}^{n} z_i\]

$\bar{z}$ is the average z-score of the profile vector, and when $\bar{z} \approx 0$ the profile is objectively normal. But as the value of $\bar{z}$ goes to positive or negative infinity (i.e. $\bar{z} \to +\infty$ and $\bar{z} \to -\infty$) then the normality is also decreasing, and the profile is becoming objectively abnormal. This additional normality measure makes the standard normal or z-score a superior normalization method.

Weighted Features

An additional issue that may require attention is the actual weights of each feature in the standard normal profile vector. While it is beyond the scope of this first article, it is worth mentioning that at some point, it may be necessary to consider that: not all features are created equally. Meaning that not all the features in the profile vector should be considered with the “same weight.” The simple solution to this, is to introduce a weight vector $W$ that can be used to apply the necessary weights to the z-score profile vector $Z$:

\[\begin{align*} \mathbf{Z}, \mathbf{W} &= \begin{bmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \\ \vdots \\ z_n \end{bmatrix} , \;\; \begin{bmatrix} w_1 \\ w_2 \\ w_3 \\ w_4 \\ \vdots \\ w_n \end{bmatrix} \\ \\ \mathbf{Q} &= \mathbf{Z} \cdot \text{diag}(\mathbf{W}) \\ &= \begin{bmatrix} \\ z_1 \\ z_2 \\ z_3 \\ \vdots \\ z_n \end{bmatrix} \begin{bmatrix} w_1 & 0 & 0 & \cdots & 0 \\ 0 & w_2 & 0 & \cdots & 0 \\ 0 & 0 & w_3 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & w_n \end{bmatrix} \\ &= \begin{bmatrix} z_1 w_1 \\ z_2 w_2 \\ z_3 w_3 \\ \vdots \\ z_n w_n \end{bmatrix} \\ &= \begin{bmatrix} q_1 \\ q_2 \\ q_3 \\ \vdots \\ q_n \end{bmatrix} \end{align*}\]

Here $Q$ represents the final weighted standard normal profile vector and the elements (i.e. features) $q_1$, $q_2$, $q_3$, … $q_n$ all represent the weighted z-score features from the standard normal profile vector $Z$ using the weights from $W$.

Matchmaking Application

To really tie all these concepts together and actually gain some insight into a “real-world” application, we will assume the role of a “matchmaker” running a simple dating/matching business. In this scenario, we will be working with a new client “Jane Doe” who we will attempt to find a match for using a profile of 9 features. Of course what these features are is not necessary to the example, but they will be 9 features of different scales (e.g. $[1, 100]$ or $[0, 1]$ or $[1000, 1000000]$ etc …), that will belong to distributions with different means and standard deviations, from which z-scores will be calculated. So let us begin by creating the distributions for these 9 features, followed by creating the standard normal profile vector for our client “Jane Doe”:

png

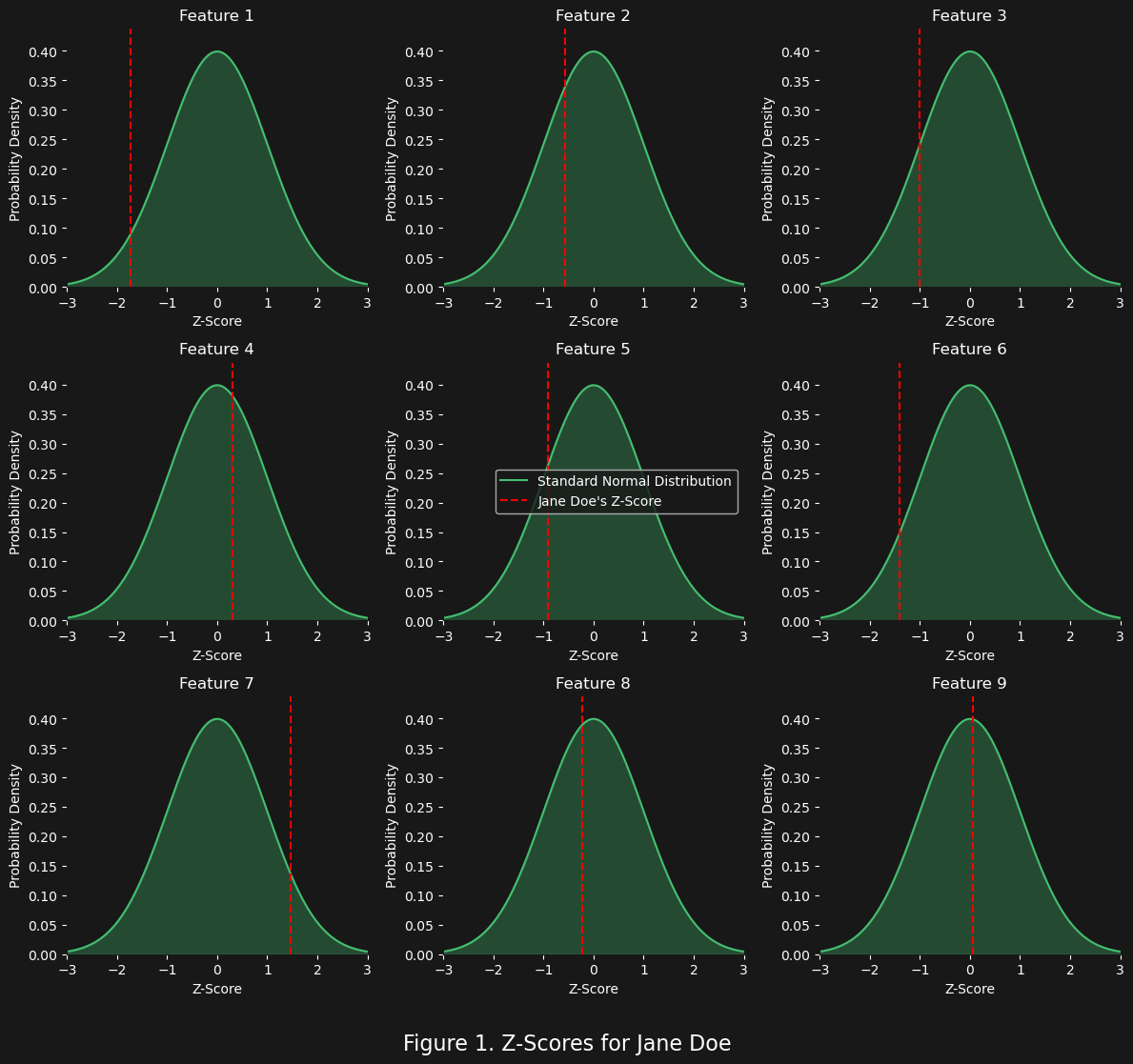
What figure 1 above shows is the corresponding z-scores $z_1$, $z_2$, $z_3$ etc … resulting from the standard normal transformation $z\left(\mathbf{R}\right)$ that maps the raw profile vector features $r_1$, $r_2$, $r_3$ … to $\mathbf{Z}$:

In other words, we are looking at the features of the standard normal profile vector $Z$:

\[\mathbf{Z} = \begin{bmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \\ \vdots \\ z_n \end{bmatrix}\]

Because the scale is the same for the standard normal distribution (i.e. the mean and stdev are all the same) this is much easier to plot than the raw distribution (where each feature has a different mean/stdev and hence a different scale).

Some of what we can see from Jan Doe’s standard normal profile is that for features $1$, $6$, and $7$ (i.e. $z_1$, $z_6$, and $z_7$) she is more than one standard deviation away from the mean. For features $3$ and $5$ she is approximately one standard deviation from the mean and feature $2$ she is approximately one half standard deviation from the mean. Finally features $4$, $8$ and $9$ she is close to the mean. This implies that, for features $1$, $6$ and $7$ she is quite deviant (objectively not normal). We would expect her match to show a similar level of deviance in these 3 features. With features $3$, $5$, and even $2$ we would expect her match to be also approximately one standard deviation. And with features $4$, $8$, and $9$ we would expect her match to also be “very normal” and close to the mean. Now let us attempt to generate some random “match profiles” and see if we can find one that is “similar” to our client Jane Doe:

png

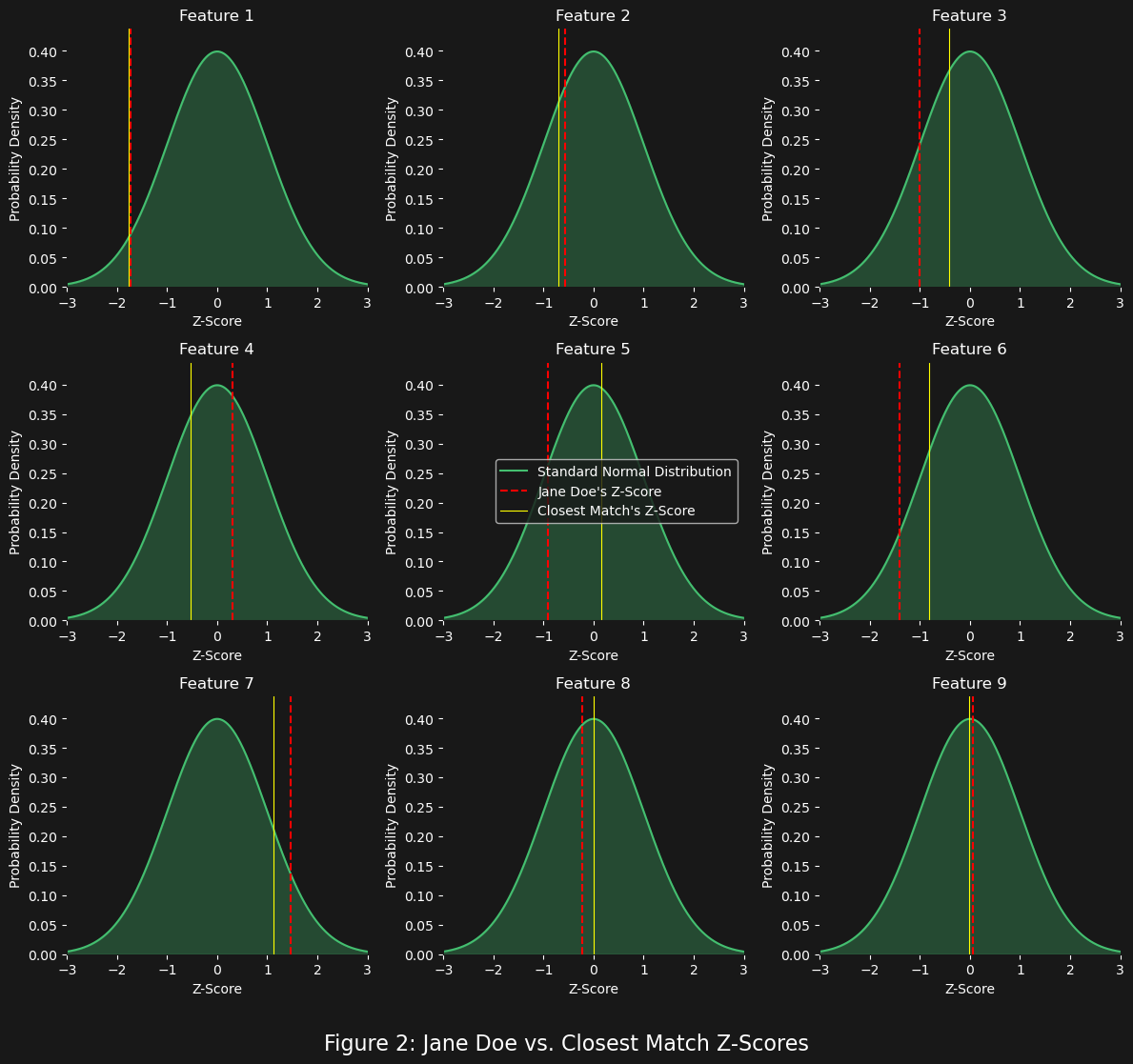
What figure 2 shows the highest ranked top 1 match (out of 1000 generated standard normal or $Z$ profiles) vs. Jane Doe (essentially the same as figure 1 but with the closest match plotted as well). The Euclidean distance was used to measure the “distance” and so the top 1 match is also the closest in “distance” to Jane Doe’s standard normal profile vector. An additional metric we could also consider is the average z-score for both Jane Doe and the top 1 closest match:

      Profile  Average Z-Score
     Jane Doe        -0.444302
Closest Match        -0.328365

It is interesting that the average z-score helps us to see what we can “generally perceive” from figure 2: Jane Doe’s closest match is still not that deviant (i.e. “abnormal”) on average as she is. What about the other top 10 z-scores?

 Profile  Average Z-Score  Euclidean Distance
Jane Doe        -0.444302            0.000000
Match  1        -0.328365            1.653682
Match  2        -0.431307            1.737071
Match  3        -0.410363            1.964756
Match  4        -0.221949            1.967314
Match  5        -0.497813            2.025522
Match  6        -0.455200            2.083044
Match  7        -0.174089            2.117304
Match  8        -0.239962            2.174969
Match  9        -0.597132            2.239997
Match 10        -0.305433            2.267270

Very interesting … so while the Euclidean distance of match 1 is the smallest, the average z-score (at $-0.328365$) is half the size of match 9 (with a value of $-0.597132$). This certainly suggests that, depending on what metric you use to “rank” the matches, you may get different results … and depending on the application, maybe average z-score would matter more than Euclidean distance.

Moral

We have only scratched the surface of the matching problem. There are many issues to consider. One obvious point is that the match criteria is arbitrary and must be tailored to each application scenario. Future work will focus more on exploring different applications, different data collection strategies, and different match criteria.